矩阵正定性的性质和判别？

吉如意hao

矩阵的正定性是线性代数中的一个重要概念，它有以下几个性质和判别方法：
### 矩阵正定性的性质：
1. "对称性"：一个矩阵是正定的，当且仅当它是对称的。 2. "自反性"：一个矩阵如果是正定的，那么它本身也是正定的。 3. "传递性"：如果矩阵 (A) 和 (B) 都是正定的，那么它们的乘积 (AB) 也是正定的。 4. "相似性"：如果矩阵 (A) 和 (B) 相似，即存在可逆矩阵 (P) 使得 (A = P^{-1}BP)，那么 (A) 和 (B) 同时是正定的或都不是正定的。 5. "交换律"：如果矩阵 (A) 和 (B) 都是正定的，那么它们的乘积 (AB) 和 (BA) 也是正定的。
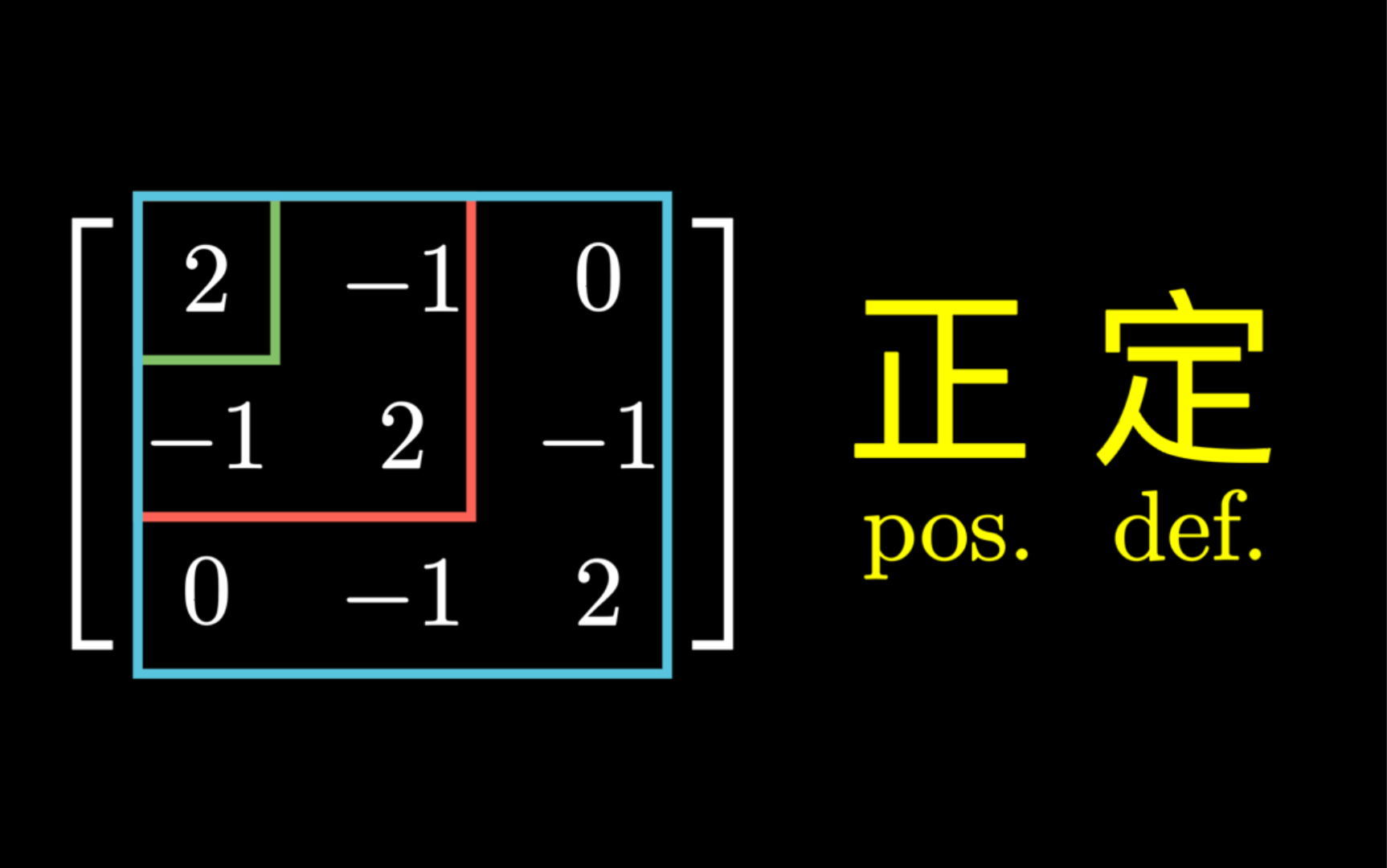
### 矩阵正定性的判别方法：
1. "特征值法"：一个实对称矩阵 (A) 是正定的，当且仅当它所有的特征值都是正的。 2. "顺序主子式法"：对于矩阵 (A)，如果它的所有顺序主子式（即由前 (i) 行和前 (i) 列构成的子矩阵的行列式）都是正的，那么 (A) 是正定的。 3. "Cholesky

端庄优雅春风NV

广义定义：设M是n阶方阵，如果对任何非零向量z，都有zTMz> 0，其中zT 表示z的转置，就称M为正定矩阵。 例如：B为n阶矩阵，E为单位矩阵，a为正实数。在a充分大时，aE+B为正定矩阵。（B必须为对称阵）。 狭义定义：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有zTMz> 0。其中zT表示z的转置。